Connectez-vous !

Cliquez ici pour vous connecter
Nouveau compte
Des millions de comptes créés
100% gratuit !
[Avantages]
- Accueil
- Accès rapides
- Imprimer
- Livre d'or
- Plan du site
- Recommander
- Signaler un bug
- Faire un lien
Recommandés :
- Jeux gratuits
- Nos autres sites
| |
Intégration Cours gratuits > Forum > Forum maths || En bas
[POSTER UNE NOUVELLE REPONSE]
[Suivre ce sujet]
Intégration
Message de alxe98 posté le 24-03-2017 à 15:27:03 (S | E | F)
Bonjour,
Je dois résoudre ce calcul intégral en utilisant une intégration par parties :
Intégrale de 1 à √2 de ln(x√2)dx.
Ja'i posé u'=1 et v=ln(x√2). Ce qui m'amène à u=x et v'=1/4x.
Pouvez-vous me dire si j'ai bon pour le moment ou si je dois recommencer (j'ai un peu de mal avec le calcul intégral).
Merci d'avance.
Réponse : Intégration de wab51, postée le 24-03-2017 à 16:06:38 (S | E)
Bonsoir
Effectivement ,on utilise une intégration par parties avec le choix suivant .
) ; ; 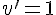 d'ou d'ou 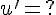 et et 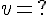 .Transmets tes réponses pour vérification .Bon courage .Transmets tes réponses pour vérification .Bon courage
-------------------
Modifié par wab51 le 24-03-2017 17:06
Réponse : Intégration de alxe98, postée le 24-03-2017 à 16:13:06 (S | E)
Merci de votre réponse.
Je ne comprends pas du=dx, je n'ai jamais vu un cas semblable.
Donc, ça veut dire que je me suis trompé pour ma dérivée dans ma précédente réponse (je m'y attendait).
Réponse : Intégration de wab51, postée le 24-03-2017 à 16:40:01 (S | E)
Excuse .J'ai oublié d'utilisé la meme notation que toi tout simplement . .Je viens de corriger dans mon 1er message .
. la dérivée de '=%5Bln(a)+ln(%7Bu%7D)%5D'=%5Cfrac%7Bu'%7D%7Bu%7D) (revois le calcul de la dérivée ,elle est fausse. (revois le calcul de la dérivée ,elle est fausse.
-------------------
Modifié par wab51 le 24-03-2017 17:11
Réponse : Intégration de wab51, postée le 24-03-2017 à 16:51:01 (S | E)
Je te rappelle l'application de la formule avec tes notations

-------------------
Modifié par wab51 le 24-03-2017 16:54
Réponse : Intégration de wab51, postée le 24-03-2017 à 17:21:01 (S | E)
Je pense que les choses sont plus claires maintenant.Sinon pose le problème ou cela n'est pas clair pour toi ? Bon courage
Réponse : Intégration de alxe98, postée le 24-03-2017 à 17:24:36 (S | E)
Mon problème avec la dérivée, c'est celui-ci.
Au dénominateur, on trouve x√2. Mais au numérateur on devrait trouver, 1/2√2, non ?
Réponse : Intégration de wab51, postée le 24-03-2017 à 18:20:20 (S | E)
On sait que la dérivée de %5D) qui est qui est %5D'=%5Cfrac%7Bu'(x)%7D%7Bu(x)%7D) Ici Ici =%5Csqrt%5B%5D%7B2%7D*x) donc donc =%5Csqrt%5B%5D%7B2%7D) d'ou d'ou %7D%7Bu(x)%7D=%5Cfrac%7B%5Csqrt%5B%5D%7B2%7D%7D%7B%5Csqrt%5B%5D%7B2%7D*x%7D=%5Cfrac%7B1%7D%7Bx%7D) . .
Sinon ,pour voir où se situe l'erreur transmets le détail de calcul pour correction .
-------------------
Modifié par wab51 le 24-03-2017 18:24
Réponse : Intégration de alxe98, postée le 24-03-2017 à 18:36:49 (S | E)
Merci pour vos explications mais c'est ça que je ne comprends pas.
Pour moi la dérivée de √2, c'est 1/2√2. Alors comment la dérivée de x√2 pourrait-elle être √2 ?
C'est certainement très idiot comme question mais je ne vois pas du tout.
Réponse : Intégration de wab51, postée le 24-03-2017 à 18:53:19 (S | E)
Il faut simplement savoir que V2 est un nombre donc une constante et la dérivée d'une constante est toujours nulle ,égale à zéro .(V2)'=0 .
Pour tout nombre réel a ,la dérivée de a est égale à zéro .
Pour ce qui est du produit a*u(x) où a est une constante (nombre réel)et u(x) une fonction en fonction de x la dérivée de [a*u(x)]'=a*u'(x). ?
-------------------
Modifié par wab51 le 24-03-2017 19:02
Réponse : Intégration de alxe98, postée le 24-03-2017 à 19:19:50 (S | E)
Merci c'est beaucoup plus clair, je pensais pas que √2 était une constante, je la dérivais comme √x.
Du coup, j'ai essayé l'intégration (même si je ne me fais pas trop d'illusions).
Je trouve :
(√2*ln(√2√2))-(1*ln(1*√2))- [1/2x^2*ln(x)]de 1 à √2 (ça c'est ma primitive)
(√2*1/2ln2+1/2ln2)-(1/2ln2)-(1/2ln2)
√2*ln2-1/2ln2-1/2ln2 =-√2
Ai-je fait beaucoup d'erreurs ?
Réponse : Intégration de wab51, postée le 24-03-2017 à 19:39:22 (S | E)
Malheureusement,la primitive est fausse .Tu as tous les outils de calcul ,il suffit de bien remplacer dans la formule générale précédente avec u=ln(V2*x) ,u'=1 ,v'=1 et v=x .Vérifie que tu dois trouver la primitive égale à A=x*ln(V2*x)-x ?Puis remplace et envoie résultat final.Je reste en connexion .
Réponse : Intégration de alxe98, postée le 24-03-2017 à 20:18:55 (S | E)
En prenant bien u=x, u'=1, v=ln(x√2) et v'=1/x et en suivant le cours à la lettre, j'obtiens bien :
L'intégrale de 1 à √2 de ln(x√2)dx = [x ln(x√2)]de 1 à √2 - l'intégrale de 1 à √2 de x * 1/x dx
Et pour moi, la primitive de x*1/x, c'est x^2*ln(x)
Je suis tout à fait prêt à admettre avoir fait une erreur mais je ne vois pas où.
Merci d'avance de me mettre sur la voie.
Réponse : Intégration de alxe98, postée le 24-03-2017 à 21:43:53 (S | E)
Alors là je suis perdu.
Je croyais que c'était justement la dérivée de ln(xracinede2) que nous avions calculé au début et qu'on avait dit que c'était 1/x, pourquoi ce serait 1?
Réponse : Intégration de wab51, postée le 25-03-2017 à 09:59:21 (S | E)
Bonjour Alex
Vraiment désolé!à cause de cette galère de connexion instable,perturbée,trop lente...depuis hier soir problème persisite encore au point elle avalait chaque fois le message que j'écrivais (4,5 6...)et voilà je retombe sur une mise à zéro .Enfin ,sans commentaire !
Reprenons donc à partir de ce message dont je porte analyse et correction
L'intégrale de 1 à √2 de ln(x√2)dx = [x ln(x√2)]de 1 à √2 - l'intégrale de 1 à √2 de x * 1/x dx (exact -parfait)
Et pour moi, la primitive de x*1/x, c'est x^2*ln(x)(faux)pour deux mise en évidence
1)x*1/x=1 (simplification simplement par x car x appartient à l'intervalle de définition Df=]0,+inf[ et par conséquent
intégrale de 1 à V2 de x*1/x dx=intégrale de 1 à V2 de 1*dx=intégrale de 1 à V2 de dx = [x]de 1 à V2 et en portant dans précédemment on obtient
A=intégrale de 1 à V2 de ln(x*V2)dx=[xln(x*V2)]de 1 à V2 - [x]de 1 à V2 .FAIRE CALCUL ET DONNER VALEUR DE A .TRANSMETS TES ESEMENTS DE CALCUL EN DETAIL POUR BONNE VERIFICATION ?
2) Dire que x*1/x est la primitive de x^2*ln(x)? revient identiquement à dire que 1( puisque x*1/x = 1)est la primitive de
x^2*ln(x)ce qui est complément aléatoire et faux .Sinon une autre preuve en calculant la dérivée de x^2*ln(x) qui est égale à
2*x*ln(x) + x^2*1/x = 2*x*ln(x)+x et on voit bien qu'elle n'est pas égale à x*1/x ou x .
Je pense qu'avec cette analyse ,j'ai répondu parfaitement à ta question et que tout est clair et je l'espère bien .
N'oublie pas de me transmettre la réponse finale de A ? Grand merci à toi Alex .
(désolé de ne pas avoir utiliser l'écriture par Latex de peur d'avoir le problème tel signalé plus haut -galère)
Réponse : Intégration de wab51, postée le 25-03-2017 à 10:09:46 (S | E)
Tu ne peux imaginer à quel point j'en suis ravi de vérifier et voir le message bien reçu au forum .Merci
Réponse : Intégration de wab51, postée le 25-03-2017 à 11:11:53 (S | E)
Ah!oui.En relisant ,je me rends compte que j'avais oublié de répondre à ta question de ton dernier message
"...,et pourquoi se serait 1"
*En fait ,c'est une erreur de frappe (revoir mon message au-dessus du 24\03\2017 à 19h39'22'')et d'ailleurs heureusement tu l'avais bien constaté qu'il s'agissait bien d'une erreur de frappe sinon comment peut-on admettre logiquement qu'en posant u'=1 et v'=1 parler d'une intégration par parties ,cela aurait supposé dire d'abord que u'=v' d'une part et d'autre part que u=v et par conséquent une étourderie peut-etre ou certes mais la réponse va de soi !Seconde preuve ,ta réponse dans ton message qui vient tout juste après ,qui montre que tu n'es pas tombé dans l'erreur en posant u'=1 , v'=1/x et ce qui exact et c'est peut-etre la cause pour laquelle ,je voulais fermer les yeux !!!Je te tire vraiment chapeau pour ta finesse et ta rigueur surtout lorsqu'il s'agit des mathématiques "sciences de la rationalité et de la rigueur .Félicitations!
Réponse : Intégration de alxe98, postée le 25-03-2017 à 11:42:40 (S | E)
Tout d'abord, je tiens vraiment à vous remercier de prendre autant de temps pour moi.
En partant de A=intégrale de 1 à V2 de ln(x*V2)dx=[xln(x*V2)]de 1 à V2 - [x]de 1 à V2, j'ai trouvé :
A=(V2*ln(V2*V2)-(1*ln(1*V2)-[x]de 1 à V2
A=(V2*lnV2+V2)-(1*ln1+lnV2)-(V2-1)
A=(V2*1/2ln2+1/2ln2)-(1/2ln2)-V2+1
A= V2*ln2-1/2ln2-V2+1
Est-ce c'est correct (j'ai toujours beaucoup de mal avec les ln) ?
Sinon, et je suis vraiment désolé si j'abuse, mais j'aimerais vraiment éclaircir deux petits points vus précédemment :
- Pourquoi la dérivée de √x c'est 1/2√x mais la dérivée de √2 c'est √2 (ou plus exactement, pourquoi √2 est considérée comme une constante) ?
- Vous avez dit que la primitive de x*1/x c'est x (je comprends très bien la logique). Simplement avant de calculer la primitive, vous avez effectué la multiplication x*1/x et ensuite, avec le résultat, vous avez trouvé la primitive. Donc je voulais savoir si nous pouvions toujours agir ainsi (faire le produit de la fonction dérivée avant de chercher la primitive) ?
C'est peut-être idiot (sûrement) mais j'aimerais beaucoup m'améliorer en maths et je donc je cherche toujours à comprendre ce qui m'échappe.
Réponse : Intégration de tiruxa, postée le 25-03-2017 à 15:19:55 (S | E)
Bonjour,
Je pense que wab51 ne m'en voudra pas si je prends un peu le relais, sinon je le prie de m'en excuser.
En partant de A=intégrale de 1 à V2 de ln(x*V2)dx=[xln(x*V2)]de 1 à V2 - [x]de 1 à V2,
j'ai trouvé :
A=(V2*ln(V2*V2)-(1*ln(1*V2)-[x]de 1 à V2 oui c'est ça
A=(V2*lnV2+V2)-(1*ln1+lnV2)-(V2-1) non car 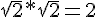
A=(V2*ln2)-(1/2ln2)-V2+1 après correction
A= V2*ln2-1/2ln2-V2+1, ton résultat était correct mais après deux erreurs qui se compensent
Réponse : Intégration de wab51, postée le 25-03-2017 à 15:27:26 (S | E)
Bonjour
De rien!Ravi de t'avoir accompagné et tout le plaisir pour moi pour tes questions intelligentes,intéressantes et pertinentes qui ont rendu ce sujet plus enviable et plus prodigieux ...J'essaierai de répondre à tes questions
1)Je sais qu'il s'agit d'une erreur de frappe (2ème ligne)au lieu de ln(V2+V2)c'est ln(V2*V2).Le résultat de A est exact.Et laisse moi te dire que tu t'en sors très bien avec les techniques de calcul des logarithmes.Et à titre arbitraire ,peut-etre voir d'écrire le résultat encore plus condensé A=(V2-1/2)*ln2 - V2 + 1 .J'essie de répondre succintement à tes deux points (tout modestement)
a)Qa- Pourquoi la dérivée de √x c'est 1/2√x mais la dérivée de √2 c'est √2?
Du point de vue écriture Vx et V2 ont la meme forme et se sont deux valeurs réels . Vx où x est une valeur écrite représentée par une lettre ,variable qui change et on peut lui attribuer n'importe quelle valeur ,on l'appelle l'invarible (ou inconnue)contrairement à V2 qui est une valeur réelle donc un nombre réel connu,fixe ,invarible et constant "c'est une constante réelle" .(Si ta question va très loin autre que cette consédération mathématique par exemple en physique,ou chimie ou autre science ,c'est une autre question pour un autre domaine ...et par conséquent je n'y peux me prétendre te satisfaire).
b)Qb-Pouvions -nous toujours agir ainsi en faisant le produit de la fonction dérivée avant de chercher la primitive ? (comme tu as fait? cas de x*1/x)
Si j'ai bien compris ta question ,je pense que j'ai déjà donné une explication en ce sens tout en justifiant le pourquoi .Est-elle la seule ? Pour moi non .Etant donné la méthode précédente me permettrait avant tout calcul de pouvoir simplifier,j'ai utilisé cette régle de simplification pour la simplicité et le raccourci des calculs. Maintenant ,si on ne simplifie et qu'on garde le produit tel qu'il est x*1/x .Je dirai que tu compliques les techniques et tu rentres dans un calcul lourd ,compliqué ...Je te donne la marche à suivre de cette méthode en pensant par calculer la primitive soit int.x*1/x *dx .D'abord ,tu auras à faire à deux intégrations par parties et deux fois un changement de variables ,en plus des compétences et des techniques de calcul .Je t'envoie par message interne ce support prochainement si tu veux .Voilà et surtout avec la chance que mon P.C.ne sait pas bloqué .Merci infiniment .
Réponse : Intégration de tiruxa, postée le 25-03-2017 à 15:45:02 (S | E)
Bon pour rebondir un peu sur ce que tu demandes, il est assez fréquent que l'on transforme une expression à intégrer, en général de produit à somme, de quotient à somme, ou aussi de quotient à produit.
En faire une liste exhaustive est impossible, souvent l'énoncé donne des indications.
Voici néanmoins quelques exemples :
Produit transformé en somme :
f(x)= (x²+5)(x²-1) = x^4 + 4x² -5
Le membre de droite s'intègre très facilement
Quotient transformé en somme :
f(x) = (x²+3)/x = x + 3/x
même remarque
Quotient transformé en produit (plus rare) :
f(x) = lnx / x = (1/x) * lnx
Le membre de droite est d type u' * u si on pose u(x)=lnx
il a pour primitve (1/2)u²
Donc une primitive sur ]0;+inf[ est F telle que F(x)= (1/2) (lnx)²
Réponse : Intégration de wab51, postée le 25-03-2017 à 15:49:50 (S | E)
Bonjour cher tiruxa
Au contraire très ravi de te voir nous tenir compagnie .Je n'ai vu ton message qu'en envoyant le mien d'où techniquement "une superpositopn"mais pour moi " d'abord une chance et c'est tout un plaisir".Je te remercie cher tiruxa .Il n'y a absolument aucun problème .Nous sommes tous engagés volontairement et bénévolement pour apporter humblement et modestement nos petites actions d'entraides pour les autres et c'est notre bonheur.Je t'en prie cher tiruxa ,il n'y a pas de frontière .Merci beaucoup Tiruxa pour ta gentillesse et ta sympathie .Sincérement ,un peu fatigué!Bonne continuation et bonne après-midi.A la prochaine.
Réponse : Intégration de zarina, postée le 25-03-2017 à 17:37:34 (S | E)
Bonjour à tous,
C'est possible de me dire en quelle classe on apprend ça et à quoi ça sert ?
Réponse : Intégration de tiruxa, postée le 25-03-2017 à 19:34:49 (S | E)
Merci beaucoup cher wab51 pour ton message tout empreint de sympathie.
Je fais de mon mieux pour répondre aux messages des intervenants comme vous autres.
Un mot pour répondre à Zarina, l'intégration s'apprend en terminale (S ou ES entre autres)
Cela sert à calculer des aires, des volumes, cela intervient aussi beaucoup en physique.
Réponse : Intégration de alxe98, postée le 26-03-2017 à 10:53:17 (S | E)
Merci infiniment à tous pour votre aide (sur ce problème) mais également pour tous vos autres enseignements. J'ai beaucoup appris avec vous.
-------------------
Modifié par alxe98 le 26-03-2017 10:53
Réponse : Intégration de zarina, postée le 26-03-2017 à 13:51:22 (S | E)
Merci beaucoup pour l'explication.
Réponse : Intégration de alxe98, postée le 28-03-2017 à 09:32:41 (S | E)
Désolé de vous déranger de nouveau mais j'aimerais une autre explication.
J'ai un nouvel exercice à résoudre, qui je crois, consiste à faire plusieurs intégrations par parties.
Il faut calculer l'aire, entre 1 et √2, contenue entre la courbe C et C' qui représentent respectivement la fonction f et la fonction g.
La fonction f = x+e^-x et la fonction g = x+√2ln(x√2).
F(x)>G(x) sur l'intervalle.
Je crois qu'il faut faire f(x)-g(x)= 2x+e^-x-2ln(x√2).
Mais pouvez-vous me dire comment commencer l'intégration parce que c'est différent du premier cas (ce n'est pas un produit).
Merci d'avance.
Réponse : Intégration de wab51, postée le 28-03-2017 à 15:32:41 (S | E)
Bonjour
C'est vraiment encore malheureux .J'ai un pépin avec ma mauvaise connexion .Elle me fait faire le travail à chaque fois!Voir dèjà lien Lien internet
Réponse : Intégration de wab51, postée le 28-03-2017 à 15:59:36 (S | E)
*1)Il me semble te signaler une contrainte dans tes données .Ce n'est pas f(x) 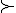 g(x) mais au contraire c'est g(x) g(x) mais au contraire c'est g(x) 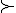 f(x) . f(x) .
-f(x)%5D.dx=%5Cint_%7B1%7D%5E%7Bsqrt2%7D%5Bx+sqrt2*ln(x*sqrt2)%5D-%5Bx+e%5E%7B-x%7D%5D.dx=sqrt2*%5Cint_%7B1%7D%5E%7Bsqrt2%7Dln(x*sqrt2).dx-%5Cint_%7B1%7D%5E%7Bsqrt2%7De%5E%7B-x%7D.dx)
*La 1ère intégrale avait été déjà faite auparavent .La 2ème intégrale qui porte la fonction exponentielle est facile à calculer avec un simple changement de variable en posant -x=X
Calcule donc cette intégrale et transmets tes résultats .Bon courage .
Réponse : Intégration de wab51, postée le 28-03-2017 à 16:23:24 (S | E)
Comme tu le constates ce topic est devenu trop chargé .Je te demande aimablement de créer un nouveau topic de cet énoncé donc de cette question ,qui me semble bien va demander certainement beaucoup d'intervention en lui donnant le titre "suite sujet intégration,en pensant à faire "copier -coller et revenir à la suppression de antécédent .Je ferai la même opération avec copie - coller pour les réponses que j'avais faites .Merci
[POSTER UNE NOUVELLE REPONSE]
[Suivre ce sujet]
Cours gratuits > Forum > Forum maths |
;
d'ou
et
.Transmets tes réponses pour vérification .Bon courage


