Connectez-vous !

Cliquez ici pour vous connecter
Nouveau compte
Des millions de comptes créés
100% gratuit !
[Avantages]
- Accueil
- Accès rapides
- Imprimer
- Livre d'or
- Plan du site
- Recommander
- Signaler un bug
- Faire un lien
Recommandés :
- Jeux gratuits
- Nos autres sites
| |
suites niveau première s Cours gratuits > Forum > Forum maths || En bas
[POSTER UNE NOUVELLE REPONSE]
[Suivre ce sujet]
Réponse: suites niveau première s de wab51, postée le 02-02-2013 à 19:15:00 (S | E)
Bonsoir bibor: As-tu essayé à répondre à la 1ère question ? Où à une quelconque autre question du problème ?Montre nous ,pour vous savoir comment nous pouvons t'aider .Poste donc tes résultats .Bon courage
Réponse: suites niveau première s de wab51, postée le 02-02-2013 à 20:04:09 (S | E)
Veux -tu bien vérifier et confirmer l'écriture de 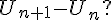 Il me semblerait bien qu'il y'a une erreur .(tu as oublié un 2 (la base de la puissance )dans les deux termes du numérateur ) . Il me semblerait bien qu'il y'a une erreur .(tu as oublié un 2 (la base de la puissance )dans les deux termes du numérateur ) .
Réponse: suites niveau première s de milarepa, postée le 02-02-2013 à 20:12:38 (S | E)
Bonsoir Bibor,
Question 1 : La méthode est la suivante :
a) Écrire Un+1
b) Écrire Un+1 - Un
c) Réduire au même dénominateur.
Où éprouves-tu une difficulté dans cette question ?
Sur ce site on ne peut faire le travail à la place des élèves, mais plutôt les orienter vers la bonne voie.
Pour les autres questions, tu peux suivre la prescription de Wab.
À toi de jouer. 
Réponse: suites niveau première s de milarepa, postée le 02-02-2013 à 20:16:27 (S | E)
Bonsoir Wab : Non, non, il n'y a pas d'erreur dans le résultat de la question 1. 
Réponse: suites niveau première s de wab51, postée le 02-02-2013 à 21:28:30 (S | E)
Bonsoir milarepa  .C'est encore plus facile que je n'imaginais . .C'est encore plus facile que je n'imaginais .  (en se référant à cette lecture ,le nombre 2 est pris comme base alors que (en se référant à cette lecture ,le nombre 2 est pris comme base alors que 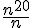 est pris comme exposant ) est pris comme exposant )
alors que la bonne écritureest la suivante :  ( rapport dans le numérateur est ( rapport dans le numérateur est 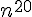 et le dénominateur est et le dénominateur est 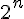 ) ) C'est pourquoi ,ma question était " il me semblerait " donc le doute ? Maintenant ,l'écriture est bien claire pour tout le monde .Je te salue bien mon cher milarepa 
Réponse: suites niveau première s de tiruxa, postée le 03-02-2013 à 10:33:03 (S | E)
Bonjour
Il y a par contre une erreur au 2 b)
C'est la suite (Vn) dont il faut donner les variations, celles de la suite (Un) ne seront étudier qu'au 3.
Dans le 1) l'étape un peu délicate est la mise au même dénominateur, il faut utiliser le fait que :
2^(n+1) = 2^n x 2
N'hésite pas à poser des questions, à condition qu'elles soient précises.
Réponse: suites niveau première s de chocho87, postée le 03-02-2013 à 12:39:06 (S | E)
j'aimerais bien de nous montrer ton essai dans cet excercice pour que je puisse t'aider, l'interet est de comprendre pour permettre de résourdre n'importe quel excercice, bon courage
Réponse: suites niveau première s de bibor215, postée le 03-02-2013 à 13:05:43 (S | E)
Bonjour à wab51, milarepa et tiruxa merci pour vos informations. j'apporte une correction dans le l'intitulé de cet exercice dans la question 2)b) les variations à étudier sont celles de (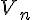 ) ) (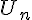 ) )
salutations
Réponse: suites niveau première s de bibor215, postée le 03-02-2013 à 16:42:58 (S | E)
bonjour à wab51, milarepa, tiruxa et chocho87 merci pour vos informations. je viens de réaliser cet exercice, voici mes réponses: question 1) démontrer 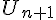 - - 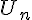 = = %5E%7B20%7D-2n%5E%7B20%7D%7D%7B2%5E%7Bn+1%7D%7D)
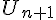 = =%5E%7B20%7D%7D%7B2%5E%7Bn+1%7D%7D)
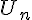 = = 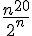
donc 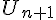 - - 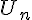 = = %5E%7B20%7D%7D%7B2%5E%7Bn+1%7D%7D) - - 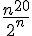 on réduit au même dénominateur %5E%7B20%7D-2%5E%7Bn+1%7Dn%5E%7B20%7D%7D%7B2%5E%7Bn%7D2%5E%7Bn+1%7D%7D) on sait que 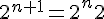 d'où %5E%7B20%7D-2%5E%7Bn%7D2n%5E%7B20%7D%7D%7B2%5E%7Bn%7D2%5E%7Bn+1%7D%7D) on simplifie par 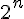 , donc , donc 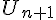 - - 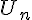 = = %5E%7B20%7D-2n%5E%7B20%7D%7D%7B2%5E%7Bn+1%7D%7D) question 2) 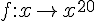
l'exposant est pair donc %20=%20f(x)) 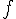 est décroissante sur est décroissante sur 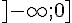
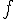 est croissante sur est croissante sur 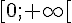
b) variations de 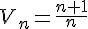 l'ensemble de définition est 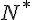 je prends 2 réels -5 et -2 sur 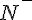 
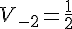
-5 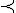 -2 et -2 et 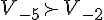 donc donc 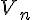 est décroissante sur est décroissante sur 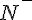 je prends 2 réels 2 et 5 sur 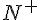 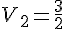
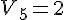
2 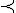 5 et 5 et 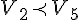 donc donc 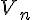 est croissante sur est croissante sur 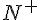 c) variations de %5E%7B20%7D) l'ensemble de définition est 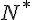 je prends 2 réels -3 et -1 sur 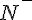 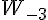 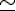 3x10 3x10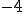
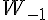 = 0 = 0
-3 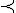 -1 et -1 et 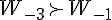 donc donc 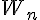 est décroissante sur est décroissante sur 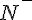 je prends 2 réels 1 et 3 sur 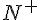 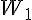 = 1 048 576 = 1 048 576
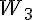 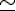 315,3 315,3
1 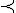 3 et 3 et 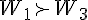 donc donc 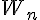 est décroissante sur est décroissante sur 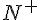 d) pour 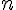 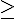 29, démontrer que 29, démontrer que 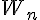 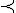 2 2 je sais que 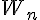 est décroissante sur est décroissante sur 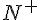 je calcule 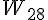 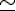 2,02 2,02 je calcule 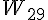 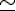 1,97 1,97 donc pour tout 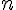 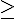 29, on a bien 29, on a bien 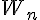 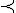 2 2 question 3) signe de 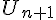 - - 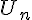 pour tout entier pour tout entier 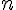 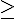 29 29 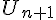 - - 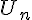 = = %5E%7B20%7D-2n%5E%7B20%7D%7D%7B2%5E%7Bn+1%7D%7D)
avec 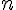 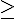 29 : 29 : 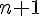
sera toujours inférieur à 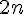 dans le numérateur donc dans le numérateur donc %5E%7B20%7D-2n%5E%7B20%7D%5Cprec%200) le dénominateur
le signe de 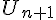 -
question 4) à partir de quel rang a-t-on :
a) 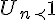 ?
pour 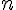 élément de (0;1) élément de (0;1) b) 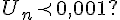
pour 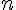 = 0
je vous remercie si vous constatez des erreurs ou manques de démonstrations
Réponse: suites niveau première s de tiruxa, postée le 03-02-2013 à 18:16:04 (S | E)
Les erreurs sont aux questions 2b et 2c puis à la 4.
En 2b et 2c, un exemple ne permet pas de démontrer un cas général, il ne peut servir que comme contrexemple !
Donc il faut procéder dans le cas général avec un n quelconque.
Par exemple en étudiant le signe de Vn+1 - Vn.
Pour la 4, on demande à partir de quel rang Un < 1, ce qui signifie que pour TOUTES les valeurs de n à partir de ce rang là on doit avoir Un < 1 !
la suite (Un) décroit certes à partir du rang 29 mais pas très vite... utilise la calculatrice pour obtenir les valeurs successives , on peut voir que U100 est voisin de 7,8, on n'est pas encore à 1 encore moins à 0,001.
Mais pour le reste c'est plutôt bien fait.
Bonne continuation
Réponse: suites niveau première s de milarepa, postée le 03-02-2013 à 18:23:31 (S | E)
Bonjour Bibor,
Q1 :  Ton calcul est juste quant au résultat (qu'on te donnait), mais pas satisfaisant méthodologiquement. En effet, puisque 2n+1 = 2n.2, quand tu réduits au même dénominateur, il est inutile de multiplier Un+1 en haut et en bas par 2n, le dénominateur commun étant directement 2n+1 (et non pas 2n2n+1 comme tu l'as écrit). Il suffit que tu multiplies Un en haut et en bas par 2. Ton calcul est juste quant au résultat (qu'on te donnait), mais pas satisfaisant méthodologiquement. En effet, puisque 2n+1 = 2n.2, quand tu réduits au même dénominateur, il est inutile de multiplier Un+1 en haut et en bas par 2n, le dénominateur commun étant directement 2n+1 (et non pas 2n2n+1 comme tu l'as écrit). Il suffit que tu multiplies Un en haut et en bas par 2.
Q2 a) :  Quel est le domaine de définition de x (il n'est pas précisé dans l'énoncé ?) ? Comment prouves-tu que la fonction f est croissante sur [0, +infini[ ? As-tu appris l'étude d'une fonction par le calcul de la dérivée ? Quel est le domaine de définition de x (il n'est pas précisé dans l'énoncé ?) ? Comment prouves-tu que la fonction f est croissante sur [0, +infini[ ? As-tu appris l'étude d'une fonction par le calcul de la dérivée ?
Q2 b) :  n appartient à N, qui est un ensemble de nombres positifs. On ne peut donc prendre des valeurs de n négatives. n appartient à N, qui est un ensemble de nombres positifs. On ne peut donc prendre des valeurs de n négatives.
Q2 c) :  On doit déduire, et pas démontrer, les variations de W. Et sur N, pas sur N-, qui n'existe pas. On doit déduire, et pas démontrer, les variations de W. Et sur N, pas sur N-, qui n'existe pas.
Q2 d) :  En admettant que tu aies démontré, dans les questions précédentes, que W est décroissante sur N (et non pas sur N+, qui n'existe pas, donc à corriger), alors ta réponse est exacte. En admettant que tu aies démontré, dans les questions précédentes, que W est décroissante sur N (et non pas sur N+, qui n'existe pas, donc à corriger), alors ta réponse est exacte. 
Q3 :  Ta démonstration n'est pas assez explicite : comment sais-tu que n+1 est toujours inférieur à 2n, et comment en déduits-tu que (n+1)20 - 2n20 est négatif ? Il ne faut pas confondre affirmation avec démonstration. Ta démonstration n'est pas assez explicite : comment sais-tu que n+1 est toujours inférieur à 2n, et comment en déduits-tu que (n+1)20 - 2n20 est négatif ? Il ne faut pas confondre affirmation avec démonstration.
Q4 a) :  Cette affirmation n'est pas démontrée. Cette affirmation n'est pas démontrée.
Q4 b) :  Idem. Idem.
Bravo pour avoir écrit tout cela.
Tu dois cependant faire preuve de plus de rigueur mathématique.
Courage, tu devrais arriver à reprendre tout cela et à maîtriser le sujet.
Cordialement.
Réponse: suites niveau première s de plumeslud, postée le 04-02-2013 à 15:13:20 (S | E)
Bonjour a tous j'ai une question qui na rien avoir avec le sujetais je voulait savoir le nivo cap correspond a quel chiffre sur ce site?merci d'avance pour vos reponses
Réponse: suites niveau première s de milarepa, postée le 04-02-2013 à 15:58:21 (S | E)
Bonjour Plume,
Il n'y a pas de chiffre ni de niveau sur ce forum *. Si tu as des questions de math (ou de physique), tu ouvres un dossier, tu exposes ta question ou ton problème et il y a toujours quelqu'un qui viendra te répondre.
Cordialement.
_______________
* Il y a également un forum pour des questions de français, et un forum anglais, etc. (il suffit que tu cliques sur l'onglet-drapeau approprié en haut de la page pour y accéder).
Réponse: suites niveau première s de bibor215, postée le 05-02-2013 à 15:52:13 (S | E)
bonjour à tous, je remercie tiruxa et milarepa pour le temps passé à me répondre. voici l'exercice corrigé en tenant compte de vos remarques : JE TRAITE LES QUESTIONS 1) et 2) a) b) c) d) LES QUESTIONS 3) et 4) SERONT DANS UN AUTRE MESSAGE PLUS TARD DANS LA JOURNEE
question 1) démontrer 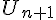 - - 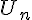 = = %5E%7B20%7D-2n%5E%7B20%7D%7D%7B2%5E%7Bn+1%7D%7D)
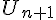 = =%5E%7B20%7D%7D%7B2%5E%7Bn+1%7D%7D)
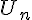 = = 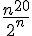
donc 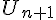 - - 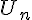 = = %5E%7B20%7D%7D%7B2%5E%7Bn+1%7D%7D) - - 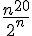
on sait que 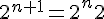 , on va réduire les deux termes de la soustraction au même dénominateur , on va réduire les deux termes de la soustraction au même dénominateur d'où %5E%7B20%7D%7D%7B2%5E%7Bn+1%7D%7D-%5Cfrac%7B2n%5E%7B20%7D%7D%7B2%5E%7Bn%7D2%7D) ce qui revient à écrire 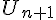 - - 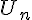 = = %5E%7B20%7D-2n%5E%7B20%7D%7D%7B2%5E%7Bn+1%7D%7D) question 2) 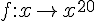
l'ensemble de définition est 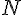 on calcule la dérivée de ) %20=%2020x%5E%7B19%7D)
) s'annule pour s'annule pour 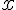 =0 =0
) est positive pour tout est positive pour tout 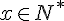
donc ) est strictement croissante sur est strictement croissante sur 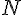
b) variations de 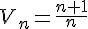 l'ensemble de définition est 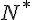 en tenant compte de la remarque de tiruxa, j'étudie le signe de 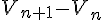 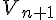 = = 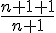 = = 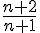
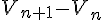 = =  = =
-(n+1)%5E%7B2%7D%7D%7Bn(n+1)%7D) =  = = 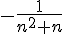
pour tout 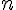 de de 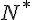 , on sait dire que , on sait dire que
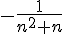 sera inférieur à 0 sera inférieur à 0
donc
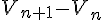 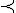 0 d'où 0 d'où  on en déduit que 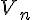 est strictement décroissante sur est strictement décroissante sur 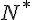
c) variations de %5E%7B20%7D) l'ensemble de définition est 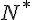
pour tout 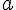 et et 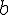 de de 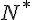 , si , si 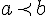 alors alors 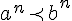 on en déduit que le sens de variation de 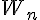 est le même que pour est le même que pour 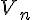 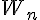 est donc strictement décroissante sur est donc strictement décroissante sur 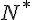
d) pour 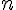 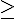 29, démontrer que 29, démontrer que 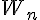 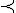 2 2 je sais que 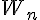 est décroissante sur est décroissante sur 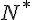 je calcule 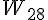 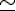 2,02 2,02 je calcule 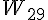 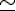 1,97 1,97 donc pour tout 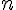 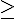 29, on a bien 29, on a bien 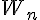 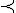 2 2 n'hésitez pas à me faire part de vos remarques.
Réponse: suites niveau première s de tiruxa, postée le 05-02-2013 à 16:56:15 (S | E)
Bon ce n'est pas parfait mais c'est déjà beaucoup mieux. 
Les petites erreurs proviennent surtout des ensembles, confusions entre N et R...
au 2a) la fonction (qui n'est pas une suite...) est définie sur R
si x > 0 , f '(x) > 0 et f(0)=0 donc f est strictement croissante sur R+
au 2b, dire simplement que la suite (Un) est strictement décroissante, c'est pour les fonctions que l'on précise un intervalle, pour les suites on peut dire le cas échéant : à partir du rang...
au 2c) c'est correct si tu remplaces l'exposant n par 20, c'est l'application du résultat du 2a)
Personnellement j'aurai plutôt écrit :
Pour tout entier n non nul :
Vn+1 < Vn donc Vn+1^20 < Vn^20 ceci d'après le 2a) et parce que (Vn) est positive
au 2d) tu peux dire qu'une suite décroissante est majorée par son premier terme à titre de justification.
Réponse: suites niveau première s de milarepa, postée le 05-02-2013 à 17:21:02 (S | E)
Bonjour Bibor,
Q1 :  
Q2 a) : Le domaine de définition de x devrait t'avoir été donné dans l'énoncé, mais je ne l'y vois pas.
Quand on considère une fonction f(x), en général, c'est R, et non pas N.
Je te recommande donc d'étudier la variation de f dans R, d'autant plus que c'est facile (ton calcul de la dérivée est juste).
Q2 b) :  La démonstration est globalement exacte. Il faut juste que tu ajoutes une ligne : « Dans N*, n étant >0, alors n2 >0 et n2+n > 0, et donc -1/(n2+n) < 0 ». (Il faut toujours éviter les évidences et les affirmations qui se font au détriment d'une démonstration.) La démonstration est globalement exacte. Il faut juste que tu ajoutes une ligne : « Dans N*, n étant >0, alors n2 >0 et n2+n > 0, et donc -1/(n2+n) < 0 ». (Il faut toujours éviter les évidences et les affirmations qui se font au détriment d'une démonstration.)
Q2 c) :  Ta démonstration est fausse. En effet, tu assimiles a et b de N* au contenu de la parenthèse de Wn, ce qui est erroné puisque ce contenu n'est pas un entier ! Donc à revoir. Je te rappelle qu'on te demande de "déduire" de ce qui précède les variations de Wn. Ta démonstration est fausse. En effet, tu assimiles a et b de N* au contenu de la parenthèse de Wn, ce qui est erroné puisque ce contenu n'est pas un entier ! Donc à revoir. Je te rappelle qu'on te demande de "déduire" de ce qui précède les variations de Wn.
Q2 d) :  
Bravo pour ta persévérance, Bibor.
Tu as avancé et tu es en train d'apprendre des éléments importants de la rigueur et de la méthodologie en mathématique.
Courage et à plus. 
-------------------
Modifié par milarepa le 05-02-2013 19:18
Réponse: suites niveau première s de bibor215, postée le 05-02-2013 à 19:17:13 (S | E)
bonjour milarepa et tiruxa, merci pour toutes ces informations. je viens de corriger la question 2) a) en remplaçant N par R 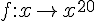
l'ensemble de définition est 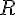 on calcule la dérivée de )
%20=%2020x%5E%7B19%7D)
) s'annule pour s'annule pour 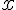 =0 =0
) est positive pour tout est positive pour tout 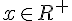
donc ) est strictement croissante sur est strictement croissante sur 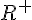 ) est négative pour tout est négative pour tout 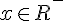
donc ) est strictement décroissante sur est strictement décroissante sur 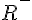
Réponse: suites niveau première s de milarepa, postée le 05-02-2013 à 19:23:55 (S | E)
Rebonjour Bibor,
Oui, c'est ok pour la question 2-a 
Tu as vu, je viens de corriger ma correction de la question 2-d.
Bonne soirée. 
Réponse: suites niveau première s de bibor215, postée le 05-02-2013 à 19:26:45 (S | E)
je viens aussi de complèter la question 2) b) b) variations de 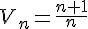 l'ensemble de définition est 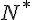 j'étudie le signe de 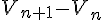 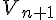 = = 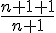 = = 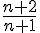
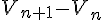 = =  = =
-(n+1)%5E%7B2%7D%7D%7Bn(n+1)%7D) =  = = 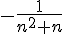
pour tout 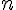 de de 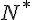 , on peut écrire que si , on peut écrire que si 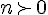 alors 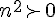 et 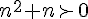 donc
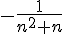 sera inférieur à 0 sera inférieur à 0
donc
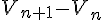 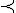 0 d'où 0 d'où 
on en déduit que 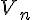 est strictement décroissante sur est strictement décroissante sur 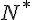
Réponse: suites niveau première s de tiruxa, postée le 05-02-2013 à 20:00:14 (S | E)
Juste un mot en vitesse... à la question 3) pense au résultat final de la 2 et transforme le.
Réponse: suites niveau première s de milarepa, postée le 05-02-2013 à 20:06:29 (S | E)
Ok pour la Q2 b)  
Réponse: suites niveau première s de bibor215, postée le 05-02-2013 à 20:26:44 (S | E)
à l'attention de tiruxa et milarepa je viens de corriger la question 2) c) c) variations de %5E%7B20%7D)
l'ensemble de définition est 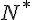
on peut écrire que 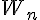 = = %5E%7B20%7D)
de la question précédente et pour tout entier 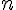 non nul on peut dire que : non nul on peut dire que : 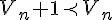 donc donc %5E%7B20%7D%20%5Cprec%20(V_%7Bn%7D)%5E%7B20%7D)
on en déduit que que 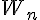 est strictement décroissante comme est strictement décroissante comme 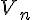
je suis un peu perdu avec les questions 3) et 4) je ne sait pas comment m'y prendre
Réponse: suites niveau première s de milarepa, postée le 05-02-2013 à 21:41:32 (S | E)
Ok pour la Q2 c)  
Q3 : On veut seulement le signe de Un+1 - Un, c'est-à-dire le signe de [(n+1)20 - 2n20]/2n+1, À PARTIR de ce qui précède.
Il faut donc :
1- que tu retrouves l'expression de Wn dans cette dernière expression,
2- ET que tu appliques le résultat de la Q2 d).
Courage !
[POSTER UNE NOUVELLE REPONSE]
[Suivre ce sujet]
Cours gratuits > Forum > Forum maths |
) définie pour tout
dans
par
=
dans
l'égalité :
-
=
) et (
) définies pour tout
dans
par
et
)
)
supérieur ou égal à 29, on a
pour tout entier
supérieur ou égal à 29
Il me semblerait bien qu'il y'a une erreur .(tu as oublié un 2 (la base de la puissance )dans les deux termes du numérateur ) .


 .C'est encore plus facile que je n'imaginais .
.C'est encore plus facile que je n'imaginais . (en se référant à cette lecture ,le nombre 2 est pris comme base alors que
est pris comme exposant )
( rapport dans le numérateur est
et le dénominateur est
)

)
)

 Ton calcul est juste quant au résultat (qu'on te donnait), mais pas satisfaisant méthodologiquement. En effet, puisque 2n+1 = 2n.2, quand tu réduits au même dénominateur, il est inutile de multiplier Un+1 en haut et en bas par 2n, le dénominateur commun étant directement 2n+1 (et non pas 2n2n+1 comme tu l'as écrit). Il suffit que tu multiplies Un en haut et en bas par 2.
Ton calcul est juste quant au résultat (qu'on te donnait), mais pas satisfaisant méthodologiquement. En effet, puisque 2n+1 = 2n.2, quand tu réduits au même dénominateur, il est inutile de multiplier Un+1 en haut et en bas par 2n, le dénominateur commun étant directement 2n+1 (et non pas 2n2n+1 comme tu l'as écrit). Il suffit que tu multiplies Un en haut et en bas par 2.


