Connectez-vous !

Cliquez ici pour vous connecter
Nouveau compte
Des millions de comptes créés
100% gratuit !
[Avantages]
- Accueil
- Accès rapides
- Imprimer
- Livre d'or
- Plan du site
- Recommander
- Signaler un bug
- Faire un lien
Recommandés :
- Jeux gratuits
- Nos autres sites
| |
Dm résolution d'inéquation
Cours gratuits > Forum > Forum maths || En bas
[POSTER UNE NOUVELLE REPONSE]
[Suivre ce sujet]
Dm résolution d'inéquation
Message de ora25 posté le 19-03-2012 à 10:47:29 (S | E | F)
Bonjour
J'ai bien besoin de vos explications, afin de pouvoir en faire d'autres par moi même s'il vous plaît.....
Je n'arrive pas à résoudre ces inéquations, quand il y'a le carré ou quand c'est au cube
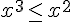
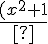(x-2)%7D%7B(2-x)(3-2x)%7D%20%5Cleq0)
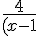%5E2%7D%20%20%20%5Cgeq%20%200)
Merci pour toutes vos explications
-------------------
Modifié par bridg le 19-03-2012 10:49
Réponse: Dm résolution d'inéquation de nick94, postée le 19-03-2012 à 11:47:45 (S | E)
Pour la 1°/
1) Regroupe tout du même côté (pour laisser 0 de l'autre)
2) factorise
3) fais un tableau de signes
Pour les 2 suivantes, le tableau de signes peut être fait directement.
Rappel sur les tableaux de signes :
Lien internet
Réponse: Dm résolution d'inéquation de ora25, postée le 19-03-2012 à 13:08:05 (S | E)
x^3 - x^2 inf ou égal à 0
x(x^2 - x)
x = 0
x^2 - x
x(x-1)
x-1 = 0
x= 1
est ce que j'ai juste????
Réponse: Dm résolution d'inéquation de nick94, postée le 19-03-2012 à 13:45:16 (S | E)
Tu as bien regroupé et factorisé mais ensuite tu as cherché les solutions de :
 - x² = 0 - x² = 0
alors que l'on te demande de résoudre :
 - x² < 0 - x² < 0
Etudie le lien que je t'ai proposé sur les tableaux de signes
Réponse: Dm résolution d'inéquation de ora25, postée le 19-03-2012 à 18:25:36 (S | E)
Voici le tableau que j'ai essayé de faire, je ne sais pas vraiment si mes données que je dois représenter sur le tableau sont bons
x |
-oo 0 1 +oo |
x |
- |
+ |
+ |
x -1 |
- |
- |
+ |
x3 - x2 |
+ |
- |
+ |
Réponse: Dm résolution d'inéquation de nick94, postée le 19-03-2012 à 18:53:44 (S | E)
L'idée est bonne mais ce n'est pas x qui est en jeu mais x², quantité toujours positive ou nulle.
Il faut ensuite lire le tableau pour donner l'ensemble solution.
Réponse: Dm résolution d'inéquation de ora25, postée le 19-03-2012 à 22:46:14 (S | E)
Quand je l'ai factorisé cela m'a donnée
x(x^2-x)
si j'avais une inéquation comme celle ci je l'aurais fait
exemple (2x-5)(-x+3)< 0
2x-5 = 0
x = 5/2
-x+3 = 0
x = 3
là je sais que ce sont ces deux valeurs de x que je dois mettre dans le tableau pour trouver le signe de (2x-5)(-x+3)
mais pour les x^3 et x^2 je bloque grave....
j'ai vraiment besoin d'aide
Bonne nuit et à Demai
Réponse: Dm résolution d'inéquation de nick94, postée le 20-03-2012 à 08:00:52 (S | E)
on a bien :
 - x² = x ( x² - x) qui n'est pas très exploitable - x² = x ( x² - x) qui n'est pas très exploitable
mais aussi :
 - x² = x² (x - 1) que je pensais que tu avais obtenu - x² = x² (x - 1) que je pensais que tu avais obtenu
peux-tu terminer maintenant ?
Réponse: Dm résolution d'inéquation de ora25, postée le 20-03-2012 à 21:59:21 (S | E)
bonjour nick94
je l'ai repris
x²(x-1)
x -oo 1 +oo
x² + +
x-1 - 0 +
x²(x-1) - 0 +
vous le vérifiez
bonne nuit à demai
Réponse: Dm résolution d'inéquation de nick94, postée le 20-03-2012 à 22:45:39 (S | E)
Il manque "0" qui annule x² et fera partie de l'ensemble solution que tu n'as pas donné.
Réponse: Dm résolution d'inéquation de ora25, postée le 21-03-2012 à 10:37:39 (S | E)
Bonjour nick94
Merci vraiment pour ton aide et tout le temps que tu consacres pour m'expliquer
Je voudrais surtout savoir comment utiliser x dans les situations suivantes:
si je dois les représenter dans un tableau de signe
(x-1)²
(x+1)²
x²-1
x²+1
x²-4
x²+4
x²-3
x²+3
Pour x^3-x^2 inf ou = à 0
x^2(x-1) inf ou = à 0
x -oo 0 1 +oo
x² + 0 + +
x-1 - - 0 +
x²(x-1) - 0 - 0 +
Bonne journée
Réponse: Dm résolution d'inéquation de nick94, postée le 22-03-2012 à 09:03:17 (S | E)
Bonjour oraz25
Pour  - x², ton tableau est correct, que proposes-tu comme ensemble solution ? - x², ton tableau est correct, que proposes-tu comme ensemble solution ?
En ce qui concerne : (x-1)²;(x+1)²; x²-1 ; x²+1 ; x²-4 ; x²+4 ; x²-3 ; x²+3
deux cas se présentent : certaines expressions ont un signe constant (éventuellement, elles s'annulent)d'autres non. Peux-tu les classer en 2 groupes ?
Réponse: Dm résolution d'inéquation de ora25, postée le 22-03-2012 à 21:58:27 (S | E)
Bonjour nick94
Pour la solution de:
x^3-x^2 ≤ 0
S = ]-oo;0]U[0;1] ou S = ]-oo;1]
En ce qui concerne : (x-1)²;(x+1)²; x²-1 ; x²+1 ; x²-4 ; x²+4 ; x²-3 ; x²+3
deux cas se présentent : certaines expressions ont un signe constant (éventuellement, elles s'annulent)d'autres non. Peux-tu les classer en 2 groupes ?
Je vais essayer:
Donc
1er groupe
(x-1)²
(x+1)²
2ème groupe
x²-1
x²+1
x²-4
x²+4
x²-3
x²+3
Merci beaucoup
Bonne nuit
Réponse: Dm résolution d'inéquation de nick94, postée le 22-03-2012 à 23:01:53 (S | E)
d'accord :
S = ]-oo;1]
En revanche, je ne suis pas d'accord avec ta répartition, il reste des expressions qui ont un signe constant dans ton deuxième groupe. Peux-tu les débusquer ?
Réponse: Dm résolution d'inéquation de ora25, postée le 23-03-2012 à 10:19:53 (S | E)
Bonjour
d'autres qui ont des signes constants
x²-1
x²+1
Réponse: Dm résolution d'inéquation de nick94, postée le 23-03-2012 à 15:40:02 (S | E)
C'est inexact pour l'un des deux et il en manque, comment as-tu fait pour les sélectionner ?
Réponse: Dm résolution d'inéquation de ora25, postée le 23-03-2012 à 17:45:48 (S | E)
Honnêtement je n'ai pas compris ceux qui sont constants et ceux qui ne le sont pas...j'ai essayé de répondre selon ma conscience....si vous voulez bien m'expliquer comment on fait s'il vous plaît???
Merci
Réponse: Dm résolution d'inéquation de nick94, postée le 23-03-2012 à 18:06:17 (S | E)
Que penses-tu du carré d'un nombre ?
Réponse: Dm résolution d'inéquation de ora25, postée le 23-03-2012 à 21:49:47 (S | E)
Le carré d'un nombre est toujours positif.
Réponse: Dm résolution d'inéquation de nick94, postée le 24-03-2012 à 11:48:31 (S | E)
Le carré d'un nombre est toujours positif ou nul.
En utilisant cette remarque, peux-tu maintenant trouver les expressions qui ont un signe constant ?
Réponse: Dm résolution d'inéquation de ora25, postée le 24-03-2012 à 11:54:32 (S | E)
Bonjour
Ceux qui sont constant sont:
(x-1)²
(x+1)²
x²-1
x²-4
x²-3
Réponse: Dm résolution d'inéquation de nick94, postée le 24-03-2012 à 11:58:55 (S | E)
(x-1)² et (x+1)² oui
pour les autres non.
je te donne un exemple :
x² - 1 = -1 (<0) si x = 0
x² - 1 = 3 (>0) si x = 2
Réponse: Dm résolution d'inéquation de ora25, postée le 24-03-2012 à 12:39:42 (S | E)
si x = -1 x<0 alors x²-4 = -3 si x=2 x > 0 alors x²-4 = 0
Donc elle n'est pas constante parce qu'elle peut être négatif dans ces cas là...c'est ça???
et pour (x-1)²
si x=-2; x<0 (x-1)² = 3
et si x=1 x>0 (x-1)² = 0
et si x = 3 x>0 (x-1)² = 4
Donc ici x est positif ou nul dans tous les cas
Réponse: Dm résolution d'inéquation de nick94, postée le 24-03-2012 à 12:48:19 (S | E)
si x = -1 x<0 alors x²-4 = -3 si x=2 x > 0 alors x²-4 = 0
Donc elle n'est pas constante parce qu'elle peut être négatif dans ces cas là...c'est ça???
et c'est pareil pour x² - 3, il faut factoriser ces expressions en utilisant : a² - b² = ....
pour (x-1)²
si x=-2; x<0 (x-1)² = 3
et si x=1 x>0 (x-1)² = 0
et si x = 3 x>0 (x-1)² = 4
Donc ici x est positif ou nul dans tous les cas
ce n'est pas en calculant pour 3 valeurs que tu prouves qu'une propriété est toujours vraie ; en revanche en remarquant que : (x-1)² et (x+1)² sont des carrés tu peux affirmer qu'ils sont toujours positifs ou nuls.
Et que dire de :
x²+1 ; x²+4 et x²+3 ?
Réponse: Dm résolution d'inéquation de ora25, postée le 24-03-2012 à 13:04:28 (S | E)
pour x²+1
x=-1 x<0 alors x²+1= 2 et si x=2 x²+1=5
Donc x²+1; x²+4 et x²+3 sont constants
Réponse: Dm résolution d'inéquation de ora25, postée le 24-03-2012 à 14:29:10 (S | E)
est ce que j'ai bien répondu à la questio
Réponse: Dm résolution d'inéquation de nick94, postée le 24-03-2012 à 17:08:25 (S | E)
pour x²+1
x=-1 x<0 alors x²+1= 2 et si x=2 x²+1=5
Donc x²+1; x²+4 et x²+3 sont constants
ce n'est pas en calculant pour 2 valeurs que tu prouves qu'une propriété est toujours vraie ; en revanche, en remarquant que : x² + 1, x² + 2 et x² + 3 sont la somme d'un carré (positif ou nul)et d'un nombre positif, tu peux affirmer qu'ils sont tous strictement positifs.
Réponse: Dm résolution d'inéquation de ora25, postée le 24-03-2012 à 18:16:27 (S | E)
donc si j'ai
(1-x)(1+x)(1+x²) ≥ 0
je fais
1-x = 0
x=1
1+x=0
x=-1
x -oo -1 0 1 +oo
1-x + + + 0 -
1+x - 0 + + +
1+x² + + + +
Produit - 0 + 0 + 0 -
S = [-1;0]U[0;1]
si c'est bon, est ce que je peux l'écrire S = [-1;1]
Réponse: Dm résolution d'inéquation de nick94, postée le 24-03-2012 à 18:39:14 (S | E)
S = [-1;1]
est bien l'ensemble solution.
Ton tableau est correct (sauf la deuxième valeur 0 sur la dernière ligne) et tu n'as aucune raison d'y faire apparaître 0 puisque 0 n'est pas une valeur qui annule une des expressions.
Réponse: Dm résolution d'inéquation de ora25, postée le 25-03-2012 à 09:26:03 (S | E)
Bonjour nick94
Merci de m'avoir aidée, surtout pour les explications et toutes les remarques.
bonne journée
Réponse: Dm résolution d'inéquation de nick94, postée le 25-03-2012 à 13:50:09 (S | E)
Bonne journée à toi aussi et continue tes efforts, les progrès sont assurés.
[POSTER UNE NOUVELLE REPONSE]
[Suivre ce sujet]
Cours gratuits > Forum > Forum maths |


